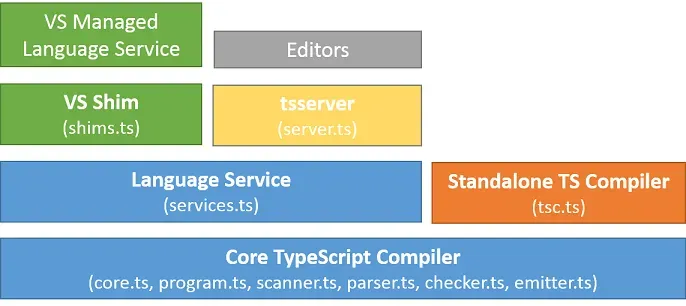
TypeScript 的类型系统
在 2017 年,TypeScript 已经占领了前端非原生语言市场的主导地位。node 的后继者 deno 也是构建在 TypeScript 之上的。本文将介绍类型系统为我们带来了什么好处,然后从集合的角度探一探类型系统的究竟,并介绍 TypeScript 在可靠性和生产力之间做了哪些平衡。
〇、TS 是什么
考虑这样一段 JS 代码。你能一眼看出其中的问题吗?
const users = [
{ id: 1, name: 'alice' },
{ id: 2, name: 'bob' },
{ id: 3, name: 'cathy' },
{ id: 4, name: 'daniel' },
];
function renderUser(id, name) {
return `<div id="${id}">${name.toUppercase()}</div>`;
}
const html = users.map((x) => renderUser(x.name, x.id)).join('\n');
JS 的松散语法给我们带来便利的同时,也带来了一些隐患:一些(通常是低级的)错误,要等到运行时才会抛出来。在上边的例子中很明显,在调用 renderUser 时,传入的参数顺序反了。
JS 的值,数字归数字、对象归对象、本身都是有类型的,但这种类型是隐式的、可变的。Python 之禅有一条是说:显式优于隐式,如果有一种办法显式地把类型告诉我们的机器,机器是不是能反馈给我们一些好处?
于是人们发明了 JSDoc,用 /** @type */ 注释来标记类型。一些代码编辑器开始跟进,以提供更好的代码检查与智能提示。然而 JSDoc 并没有一个标准规范告诉人们 @type 后面写什么,因为它更偏重于文档功能;而且标注函数和复杂对象时显得力不从心。所以 JSDoc 不能说是一流的类型解决方案。
如果我们觉得有必要做类型,是不是可以考虑把类型放在更显著的位置上,比如创造一些额外语法来支持类型?这个思路下的解决方案,就是本文的主角 TypeScript(以下简称 TS)。

我们为函数 renderUser 的入参标注好类型之后,TS 立刻检测出了第 11 行的参数类型错误。注意,我们并没有标注过 users 的类型,它的类型乃至第 11 行 x 的类型都是根据先前赋值自动推断出来的。
同样在第 11 行可以注意到,在键入 x. 之后,编辑器已经给出了提示:x 有两个属性 id 和 name。精确的自动补全功能,是类型系统带来的额外便利。
一个用当前文档中的词语实现的自动补全功能,像是从原始时代来的。 —— Felix Rieseberg
另外,TS 还帮我们检查出了第八行的笔误。笔误严格说来属于类型错误,不过更进一步:TS 会在已知的的属性名或方法名中寻找可能存在的正确名称。
有了类型加成之后,重构代码变得如此轻松:

以上,相信即使是初见者也能快速明白 TS 的两大好处:防患于未然的静态检查,以及干净利落的智能提示。这一切都是建立在它的类型系统之上的。
如何玩转示例代码?两种方案二选一:
- 在线
- 打开 http://www.typescriptlang.org/play/index.html ;
- 点击 Options 把选项全部勾选上;
- 贴入示例代码到左侧文本框。
- 本地
- 安装 VS Code;
- 新建一个空文件夹,在里边创建一个
tsconfig.json文件,其内容为{ "compilerOptions": { "strict": true } };- 创建
index.ts文件,贴入示例代码。
一、类型是什么
类型是所有满足某些特征的 JS 值的集合。举个例子,number 类型,是所有浮点数、NaN、±Infinity、-0 的集合。
我们知道,集合具有下列三个特征:
- 确定性:给定一个元素,可以明确地判断其是否属于该集合。
- 互异性:集合中不存在两个相同的元素。
- 无序性:集合中的元素任意排列,仍然表示相同的集合。
在一个类型中,我们不关心值的次序,也不存在重复的值。由于类型是用代码精确地定义的,那么 TS 语言服务总能判断一个值是否满足某个类型的要求。
事实上,要精确地判断一件事物是否是集合,需要一堆抽象的废话。自从罗素悖论被提出后,人们才发现朴素集合论自身的矛盾性。现在为了定义集合,应用最广的是 ZF 公理系统。其中有一条分离公理:一个集合(所有 JS 的值,由 ECMA 规范定义)中,抽出所有满足某命题的元素(TS 判断是否满足某类型),可以构成一个新的集合。
集合的外延与内涵
一个集合可以从外延和内涵两个方面来看待。谈到外延时,指的集合中一切元素的全体:整数集的外延就是 {..., -2, -1, 0, 1, 2, ...}。谈到内涵时,指的是集合中所有元素的公有属性:整数集的内涵是每个元素都能被 1 整除。
整数集中去掉所有负数后,就有了新的内涵:每个元素都大于等于 0 。一个集合的外延越小,其内涵越多,反之亦然。
二、类型速览
原始类型
对应 JS 的原始类型,TS 提供了如下几种原始类型:
number:包括浮点数,以及NaN、±Infinity。string:字符串型。boolean:布尔型,即 false。null:即 null。undefined:即 undefined。symbol:符号类型。
TS 还提供了类型 void,它等于 undefined。
另外,所有原始类型的字面量本身也可作为类型使用,其外延只包括自身。

对象类型
通过类似 JS 对象字面量的方式来定义类型。
type point2D = {
x: number;
y: number;
};
const center: point2D = { x: 0, y: 0 };
对象的键也可以不精确到特定键名:
type httpHeaders = {
[key: string]: string | undefined; // "|" 表示“或者”
};
这表示对于 httpHeaders 类型的值,以任意字符串作下标取值都是合法的,值的类型为字符串或者 undefined。
函数类型
函数类型分为两种,普通调用和构造调用,其区别在于调用时是否带有 new 关键字。
type unary = (x: number) => number;
type newPoint = new (x: number, y: number) => point2D;
type returnSelf = {
// 多态的函数
(x: string): string;
(x: number): number;
};
这里我们暂时不要关心上述函数类型的具体实现。unary 类型是数字的一元运算,Math 库里的许多函数都是此类型,如 Math.sin、Math.abs 等。newPoint 类型表示用两个坐标构造出 point2D 的构造函数。string ∪ number 集合上的恒等映射就满足 returnSelf 类型。
签名(Signature)
对象类型的单一属性、单一函数类型叫做一条签名。例如上文中 point2D,x: number 就是它的一条签名。介绍此概念,是为了下文更方便地理解子类型。
签名(Signature)分为三种,call, construct 和 index,分别对应上述的普通调用、构造调用和对象类型。它们的形式是类似的:
/** 确实存在 strangeThing 类型的对象! */
/** f 就满足 strangeThing 类型。
function f(x) {
if (this.constructor === f) return {}
return x
}
f.foo = 'bar'
*/
type strangeThing = {
foo: string; // index
(x: number): number; // call
new (): {}; // construct
};
/** 可以认为每一行签名就是类型的内涵。 */
签名可以类比成集合间的映射。 它把冒号左边的原像集、连同签名方式,映射到右边的像集。
三、类型运算
联合类型
示例中,text 称作 string 和 number 的联合类型。一个 text 类型的变量,既可以被赋值为字符串,又可以被赋值为浮点数。

也就是说,text 作为集合是 string 和 number 的并集。两个集合的并集,其内涵只包括原来两个集合的共有内涵。
对于一个 string 类型的变量,我们可以访问它的 toUpperCase、split、length 属性或方法;可以访问 number 类型变量的 toFixed、toString 等方法。而对于 text 类型的变量,我们只能访问 string 和 number 的共有方法 toString 和valueOf,其他属性或方法都不保证存在。
交叉类型
type landAnimal = {
name: string;
canLiveOnLand: true;
};
type waterAnimal = {
name: string;
canLiveInWater: true;
};
// 交叉类型:两栖动物
type amphibian = landAnimal & waterAnimal;
let toad: amphibian = {
name: 'toad',
canLiveOnLand: true,
canLiveInWater: true,
};
交叉类型的含义为:符合类型 A 和 B 的交叉类型的值,既符合类型 A,又符合类型 B。
类比前文的联合类型,交叉类型可以认为是两个类型的交集。其内涵覆盖了原来两个集合的所有内涵。
从较抽象的层面看来,你也可以认为 { x: number, y: number } 和 { x: number } & { y: number } 是一回事儿,尽管 TS 在具体实现上有细微的差异。
全集和空集
any 类型,顾名思义,泛指一切可能的类型,对应全集。
理论上,任意集合交上全集保持不变 T ∩ any = T(实际上 T & any = any,any 类型在任意运算中都是有传染性的);全集并上任意集合还是全集 T ∪ any = any。
never 类型对应空集。任何值,即使是 undefined 或 null 也不能赋值给 never 类型。对于任意类型 T, T ∩ never = never,T ∪ never = T。TS 也是如此实现的。
那么 never 类型在实际应用中如何才会出现呢?
- 一个中途抛出错误,或者存在死循环的函数永远不会有返回值,其返回类型是
never。 - 在某些情况下,TS 会将空数组推断成
never类型,这是因为在实际中,空数组经常被作为默认值使用。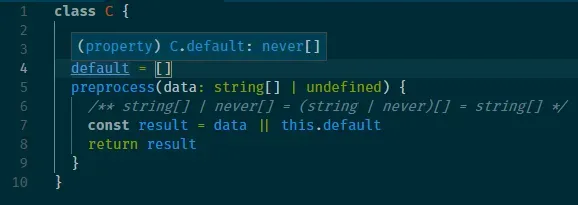
四、类型兼容性
考虑以下代码。 point2D 可以被当做 point1D 来处理,反之不行。我们说 point1D 类型兼容 point2D。
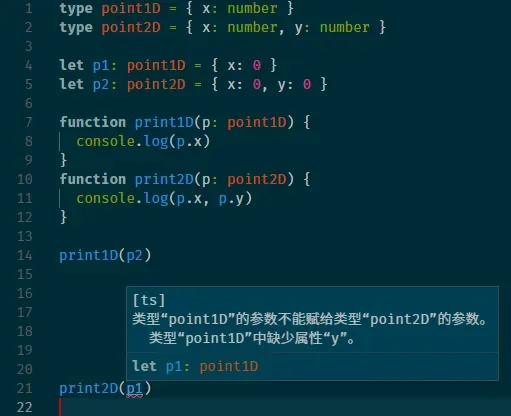
为什么?因为我们所需要的 point1D 的所有内涵(属性 x),在 point2D 中均存在;反过来,point1D 不存在属性 y。也就是说,point2D 的内涵涵盖了 point1D,是它的子集。子集的外延小于父集,内涵大于父集。
我们也可以从更加“集合论”的角度看待这个现象,作为 point1D 与另外一个类型的交集,point2D 显然是其子集。
point2D = { x: number, y: number }
= { x: number } ∩ { y: number }
= point1D ∩ { y: number }
当且仅当类型 B 是 A 的子集时,A 兼容 B,B 可以被当成 A 处理。
结构子类型
TS 采用结构子类型。其含义是:两个类型,即使表示的业务含义大相径庭,只要结构上有从属关系,就是兼容的。(“等同”也是从属关系的一种)
type Box = {
/** 箱子的容积 */
volumn: number;
};
type Speaker = {
/** 扬声器音量 */
volumn: number;
};
let box: Box = { volumn: 3000 };
let speaker: Speaker = { volumn: 20 };
box = speaker; // 允许赋值
与此相对的是名义子类型:只有显示声明的子类型才算子类型,否则即使结构相同,也不能互相赋值。C++、Java 均采用此方案。
签名
现在我们来深入处理签名的本质。前文说到,签名是集合间的映射。该如何判断两个映射之间是否有父子关系?
考虑如下四个类型。这里的 'say'、'hi' 都是类型,且是 string 的子集(子类型)。
/** 等价于 { say: string },只是在此上下文中统一了写法 */
type T1 = { [key in 'say']: string };
type T2 = { [key in 'say']: 'hi' };
type T3 = { [key in string]: string };
type T4 = { [key in string]: 'hi' };
我们来两两分析类型间的关系:
- T1、T2:假如可以用
notHi来表示所有非'hi'的字符串,那么T1 = { [key in 'say']: 'hi' } ∪ { [key in 'say': notHi },所以 T1 是 T2 的父集。 - T1、T3:假如可以把所有字符串遍历出来,那么 T3 可以写成:
{
...
sax: string
say: string
saz: string
...
}
那么 T3 的内涵比 T1 多得多,所以 T1 也是 T3 的父集。
- 类似地,我们知道 T2 是 T4 的父集,T3 是 T4 的父集。T1 作为 T2 的父集当然也是 T4 的父集。
- 那么 T2 和 T3 之间有父子关系吗?答案是没有。我们可以轻易地证明这一点:对象
{ say: 'bye' }满足 T3 但不满足 T2;{ say: 'hi', numericKey: 0 }满足 T2 但不满足 T3。
综上所述,当映射的原像集(冒号左侧)外延扩张、或者像集(冒号右侧)外延收缩时,产生一个新的子集。
函数类型
说完了签名,为什么要单独讨论函数?因为与下标索引不同的是,函数的参数长度是可变的。
如果调用时传入的参数多于定义时所需的,那么多余的参数会被无情忽视。考虑这个函数:
function f() {
return 0;
}
f(); // 0
f(0); // 0
f('hahaha'); // 0
f(null, false, {}, 233); // 0
我们知道 f 的类型是 () => number,问题:类型 () => number 和 (x: number) => number 是什么关系?
为了便于理解,考虑一种等价形式:观察函数的参数数组(arguments)和返回值的关系。那么 f 的类型等价于 (args: {}) => number,后者的类型等价于 (args: { 0: number }) => number。
这样把 0 个或多个参数考虑成一个参数,就可以应用上节结论:当函数新加一个参数定义时,也就增加了一条原像集的内涵,收缩了其外延,得到原函数类型的父集。
总结一下,当一个签名类型:
- 增加一条签名;
- 扩展某条签名的原像集外延;
- 删掉一个函数签名的尾部参数(扩展了原像集外延);
- 收缩某条签名的像集外延;
都是增加了其内涵,得到了一个子类型。
五、平衡
有人会问了,知道怎么判断子类型有意义吗?TS 不就是帮我们做这件事情的吗?这句话并不全对。翻开 TS 的设计初心,Non-goals 的第三条赫然写道:
TS 的设计目标不是为了提供一个学术意义上严谨的类型系统,而是力图达到严谨性和生产力的平衡。
像 Elm 的类型系统就是严谨性的极端,它声称可以完全避免运行时错误。但在实际使用中,这种严谨性会损害生产力,因为它强迫开发者做很多边界处理,尽管这些边界情况被达到的频率未必值得花时间去处理。
很多时候 TS 会为了实用性,允许一些不严谨的操作。下面我将一一举例,希望读者今后在使用 TS 时,能做到心中有数。
这些不是 bug,是 feature。
any 和 never
any 类型本来没有任何实质内涵,所以访问一个 any 类型变量的任意属性或方法都是不可靠的。然而 TS 引入 any 类型却恰恰是为了允许随意访问某变量。常见情况是,在一个 TS 项目中引入一个没有类型的第三方库,只要把这个库的入口对象声明成 any 即可。
never 类型作为另一个极端,它的内涵是无穷多的。访问 never 类型变量的任意属性都是理论上可行的,虽然没有意义,因为 never 类型并不会有实例。
函数参数中的 () => void
function expectVoid(f: () => void) {
const result = f();
return result === undefined || result === null;
}
expectVoid(() => 1); // false
逻辑上说,expectVoid 应该永远返回 true 才对,而且这里应该抛出类型错误,因为 () => void 和 () => number 并没有父子关系。
然而,TS 认为 () => number 是可以当作 () => void 来使用的。这是因为很多库的作者会把回调函数的类型写成 () => void,他们的真正意图是:“我并不关心回调函数返回什么,因为我不会处理它的值。”更为贴切的类型是 () => any。像例子中,真正期望 void 返回值的情况是极少的。
字典表
type stringMap = {
[key: string]: string;
};
let map: stringMap = {
say: 'hi',
};
map.hello.toUpperCase(); // 运行时错误!
前文中讨论过,{ say: 'hi' } 作为类型,与 { [key: string]: string } 之间是没有父子类型关系的。
TS 允许如此赋值的原因是:在实际中,处理字典表一般要先用 Object.keys 取键,再进行下一步操作。况且要是严谨起来的话,那赋值的时候要把所有的字符键名都写一遍才对,这是不可能的。
如果代码中硬编码有 hello 这个键,应该把 hello: string 这条签名单独加在类型中。
六、总结
本文用理科的视角介绍了一遍 TypeScript,并未涉及工程方面。如需了解泛型、模块、类与接口等,大部分其他文章都有介绍,或者参阅官方文档: TypeScript Handbook。